Chapter 10 Element 4: Indexing
10.1 Learning Objectives
By the end of this chapter you should be familiar with:
- Indexing using
[], and
We already encountered a type of indexing when we used the subset() function and logical expressions. Here, we will go one step further and perform indexing without using any unnecessary functions. We can filter our data-set according to:
- Equations (i.e. using logical expressions, see section 9
- Position (i.e. using row & column number, discussed here.), or
- Text matching (i.e. using regular expressions).
10.2 Indexing vectors (1D)
The beauty of indexing is that we can use [] notation for all of these types of questions. We can limit our investigation to specific data points by using the [x] notation to select the \(x{}^{th}\) data point in a vector. Let’s return to the simple foo1 example.
# [1] 1 8 15 22 29 36 43 50 57 64 71 78 85 92 99# [1] 36# [1] 6# [1] 36# [1] 15 22 29 36# [1] 15 22 29 36 43 50 57 64 71 78 85 92 99This is convenient, but becomes very powerful when we start mining our data by combining position with logical expressions. Recall that the result of a logical expression is a TRUE/FALSE answer, which can be used as an index.
# [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE FALSE FALSE
# [11] FALSE FALSE FALSE FALSE FALSE# Save the logical expression as an object and use it
# as an index to report only the TRUE results
m <- foo1 < 50
foo1[m]# [1] 1 8 15 22 29 36 43# [1] 1 8 15 22 29 36 43# Combine logical expressions to find values:
# Either less than or equal to 22 or greater than 71
foo1 <= 22 | foo1 > 71# [1] TRUE TRUE TRUE TRUE FALSE FALSE FALSE FALSE FALSE FALSE
# [11] FALSE TRUE TRUE TRUE TRUE# [1] 8# [1] 1 8 15 22 78 85 92 9910.3 Indexing Dataframes (2D)
Recall that each column in a data frame is the same as a vector. Returning to the foo_df data frame we defined earlier, let’s try to extract the same information using logical expressions instead of the subset() function.
# healthy tissue quantity
# 1 TRUE Liver 1
# 2 FALSE Brain 7
# 3 FALSE Testes 13
# 4 TRUE Muscle 19
# 5 TRUE Intestine 25
# 6 FALSE Heart 31# [1] "Liver" "Brain" "Testes" "Muscle" "Intestine"
# [6] "Heart"# [1] TRUE FALSE FALSE FALSE FALSE FALSE# [1] 1# How many Liver samples are there?
# TRUE values = 1, so take the sum.
sum(foo_df$tissue == "Liver")# [1] 1Notice that we can combine an index of one column (i.e. foo_df\$healthy == TRUE) to extract values from another (foo_df\$quantity).
# [1] 1 19 25To really make use of indexing with data frames, we can use [x,y] notation to select the $x{}^{th}$ row (i.e. observation) of the $y{}^{th}$ column (i.e. variable).
# healthy tissue quantity
# 4 TRUE Muscle 19# [1] "Muscle"10.4 Exercises for Indexing
With the tools we have introduced so far, you will be able to start data mining. Let’s begin by extracting some interesting information from the protein_df data frame. First, let’s return to the exercises from the previous chapters and see if you can answer these questions in an easier way now:
Exercise 10.1 (Find protein values) Given a list of Uniprot IDs:
- GOGA7
- PSA6
- S10AB
filter(), use [] instead.
filter(), use [] instead.
Exercise 10.3 (Find extreme values)
For the H/M ratio column, create a new data frame containing only proteins that have a \(log_{2}\) ratio above 2.0 or below -2.0. Again, try to determine this without creating a new data set or using the subset() function.
The following sections will help you to answer the previous exercises
10.5 Ordering functions
There are a couple different ways to think about sorting data. Don’t confuse the following functions:
| Function | Description |
|---|---|
sort() |
Returns a sorted vector (ascending or descending). Calls order() under-the-hood. |
order() |
Returns an index (integer vector) of the position of the ordered values (ascending or descending). Use this for data frames. Allows ordering on multiple vectors. |
rank() |
Returns the ranks of values in a vector, e.g. in non-parametric tests. |
arrange() |
Part of the tidyverse. Rearranges a variable |
# [1] "Liver" "Brain" "Testes" "Muscle" "Intestine"
# [6] "Heart"# [1] "Brain" "Heart" "Intestine" "Liver" "Muscle"
# [6] "Testes"# [1] 2 6 5 1 4 3# [1] "Brain" "Heart" "Intestine" "Liver" "Muscle"
# [6] "Testes"# healthy tissue quantity
# 1 TRUE Liver 1
# 2 FALSE Brain 7
# 3 FALSE Testes 13
# 4 TRUE Muscle 19
# 5 TRUE Intestine 25
# 6 FALSE Heart 31# healthy tissue quantity
# 1 FALSE Brain 7
# 2 FALSE Heart 31
# 3 TRUE Intestine 25
# 4 TRUE Liver 1
# 5 TRUE Muscle 19
# 6 FALSE Testes 13# healthy tissue quantity
# 1 FALSE Testes 13
# 2 TRUE Muscle 19
# 3 TRUE Liver 1
# 4 TRUE Intestine 25
# 5 FALSE Heart 31
# 6 FALSE Brain 710.5.1 Exercise for ordering
10.6 Intersection functions
To answer the last exercise you’ll need to know a bit about combining data. We saw merge functions in the section on data frames (page 7.4). Here, is another set of functions which is very useful: the intersect family. Given vectors x and y:
| Function | Description |
|---|---|
intersect(x, y) |
Values in both vectors x and y. |
setdiff(x, y) |
Values in vector x, which are not in y. |
setdiff(y, x) |
Values in vector x, which are not in y. |
union(x, y) |
Set of all unique values in vectors x and y. |
# [1] 5 6 7 8# [1] 1 2 3 4# [1] 9 10 11 12# [1] 1 2 3 4 5 6 7 8 9 10 11 1210.6.1 Exercise for Intersections
10.7 Performing Statistical Tests
R is extremely powerful when it comes to performing statistical tests. Here, we will do a Pearson’s correlation between the Log2 ratios of HM and HL. The correlation test will be done with the cor.test() function, as follows:
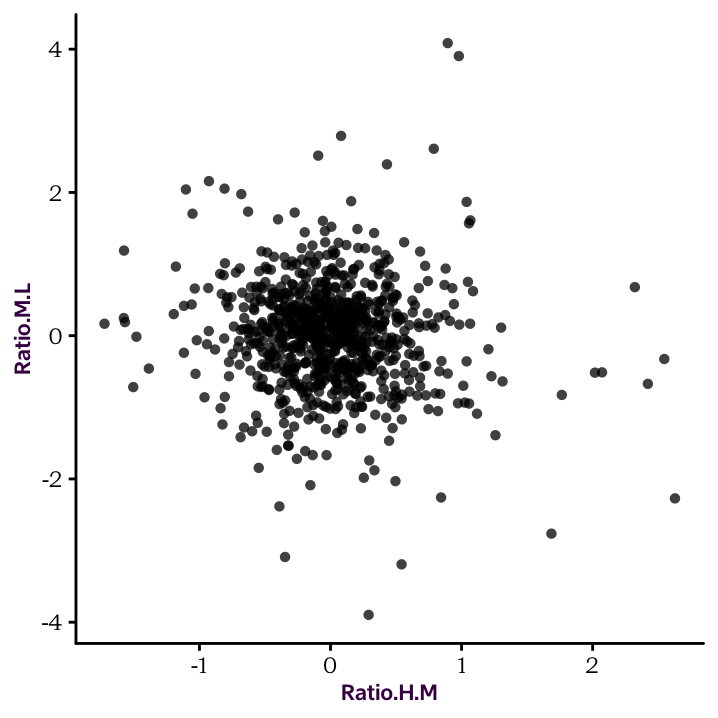
#
# Pearson's product-moment correlation
#
# data: protein_df$Ratio.H.M and protein_df$Ratio.M.L
# t = -3, df = 830, p-value = 0.01
# alternative hypothesis: true correlation is not equal to 0
# 95 percent confidence interval:
# -0.156 -0.021
# sample estimates:
# cor
# -0.089The cor.test() function provides a set of values which can be individually accessed:
# $names
# [1] "statistic" "parameter" "p.value" "estimate"
# [5] "null.value" "alternative" "method" "data.name"
# [9] "conf.int"
#
# $class
# [1] "htest"# [1] "htest"# [1] "statistic" "parameter" "p.value" "estimate"
# [5] "null.value" "alternative" "method" "data.name"
# [9] "conf.int"# [1] 0.01# cor
# -0.089# cor
# 0.008The class of a cor.test() output is htest (hypothesis test). htest objects are lists. They have some unique properties, but you can extract information in a similar way as in data frames.
Note that the default
cor.test()function performs a Pearson correlation coefficient. If we wanted to perform a Spearman’s rank-correlation coefficient, we would have to set themethodargument to"spearman". Also, in the output,correfers to \(R\). To calculate the more common \(R^2\), you will have to square it.↩︎